在自然科学的各分支学科中，数学和物理学雄踞上游。除了数学作为基本方法和工具、物理学作为基本原理这样的大致认知外，这两门学科常以严格求解科学问题来揭示本质的做派，极具震慑力、摄人心魄，也是其地位和魅力的表现。相对而言，其它基础分支学科，主体上不具有这样的特征。过去数百年来，数学和物理学，通过一波一波严格可解问题的展示，巩固和扩展其源头地位，形成一种对人有压迫感、让人心悦诚服的张力。这是 Ising 的感受，虽然可能言过其实。

　　所谓言过其实，也是针对当下风景而言。Ising 不敢轻言数学，也不敢轻言物理学中凝聚态和统计物理之外的那些分支。但大致上可体察到，数学学科中计算数学发展很快，凝聚态物理也是计算物理大行其道 (实验物理是另一个层面，在此不论)。在这样的局面下，问题严格求解就变得稀有而珍贵。Ising 当年写博士论文时，曾尝试得到一个简化版物理问题的严格解，但最后还是需要付诸数值计算才能得到结果，因为那个所谓的“严格解”包含有积分表达。这样的问题，如果依然可归类于严格可解问题 (Exactly solvable model, ESM)，严格可解问题才稍微靠近黎民百姓而不那么阳春白雪。即便如此，任何一位物理学教授，学术生涯如果能够得到一个 ESM 或者其严格解，应该算是幸事一件。正因为如此，得到重要物理问题严格可解结果的物理人，绝对值得尊敬和景仰。这是物理学的人文情怀，限于 Ising 视野狭窄而姑且用图 1 作某种意向展示。

　　如果一定要对物理问题严格可解的珍贵说出个道理来，Ising 以为，在一般性学术价值意义之外，还有两个层面：

　　第一个层面。物理问题的严格求解，毕竟是自然科学的终极梦想，也是科学人生和人文情怀的至高追求，更是学问之道的终极表现形式。这样的表达，带有很大感性成分，却并不为物理人所轻看。当然，个中道理仁者见仁智者见智，干脆在此不论了。

　　第二个层面。对凝聚态而言，严格可解，意味着可确认某个物态是否真实存在、某个物理过程是否明确可期，并可确定存在的区域和基本性质。这种确认，有时极其重要而不可替代。Ising 稍有了解一些例子，例如那个经典的二维正方晶格 Ising 模型。有关它若干性质的严格求解，都是以“定理”来定义的。当下就更别提三维 Ising 模型严格解的皇冠地位^_^。

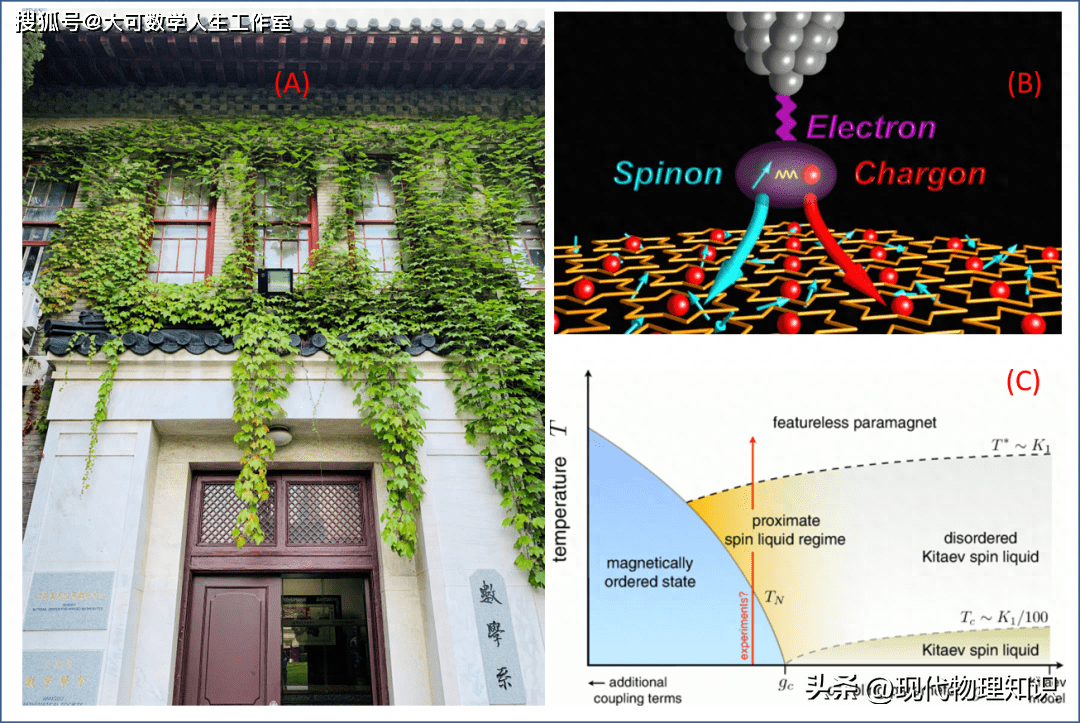
　　另一个比较当代的例子，即量子自旋液体 (quantum spin liquid, QSL)。虽然安德森很早就提出了基于共振价键 (resonating valence bond, RVB) 的形成机制，但 QSL 到底存不存在？在什么条件下存在？似乎还是一个问题。这一问题的难度在于：既然是高度无序的“液态”，无序之外还有“理想气态”中没有的自由度纠缠 (spatiotemporal entanglement)，意味着实验将不会有足够好的表征手段去标记这一物态。用非常“粗鲁”的话说，即此类“液态”，缺乏好的序参量标识，其状态及行为有点像“黑洞”一般。如此，如何去确定实验得到的物态是不是 QSL 呢？物理人当然可以竭尽所能，从实验和计算两个层面，穷举式地确认或否定 QSL。但是很显然，最简洁明快、确定无疑、一举中的地肯定或否定的判据，应该是测量结果能否与严格解结果定量吻合或不吻合。在逻辑上，这一判定相当于是要优雅地“无中生有”，而只有严格解才能终极生出“有”、最终确认一个体系是不是 QSL。

　　如上两个层面的意义与价值，在 2006 年 Alexei Kitaev 的一项了不起的工作中得到渲染。他获得了二维六角蜂窝状格子 (in-plane honeycomb lattice) 上自旋 1/2 模型有一个 QSL 的严格解，轰动凝聚态物理学界。首先，这是一个漂亮的、严格可解量子自旋模型。即便最开始认为是一个“玩具”模型，它也已足够美妙。随后，向涛和张广铭老师他们将该模型与马约拉纳费米子 (Majorana fermions) 联系起来，也是一个重要结果。模型中的 Kitaev 相互作用，又在包含晶体场、自旋 - 轨道耦合 SOC 和量子关联的 Mott - Hubbard 模型计算中得到佐证，从而赋予这一严格可解模型又一重价值，为研究 Kitaev 量子自旋液体 QSL 开启了大门。到今天，一方面，物理人将 Kitaev 当成大神一般，给予他诸多崇高学术荣誉，并再次对俄罗斯民族为物理学做出巨大贡献以敬意。另一方面，物理人将这一模型与寻找具体的 QSL 体系联系起来，使得 Kitaev 模型及其求解成为量子磁性和阻挫物理的重要方向。

　　其中，一个备受关注的方向，即如何将 Kitaev 模型推广到更为接近实际材料的情况。Ising 道听途说，得知诸多进展之一，乃来自南京大学李建新与温锦生两个团队的工作。他们针对最接近 Kitaev 模型的体系 α-RuCl3，开展了系统的理论与实验探索，给出了其中 Kitaev 耦合项的定量大小和更一般性的模型形式，引起同行关注和跟踪。虽然这一具体定量模型的严格求解可能存在一定难度，但已能够让物理人脚下之路宽广了一些。

　　当然，更多物理人可能想一举两得：既要将 Kitaev 模型推广至与实际更接近，即给模型添加更多具有明确物理意义的相互作用项，还要试图求得这些推广模型的严格解。一个很自然的推广，当然是进行三维拓展。Kitaev 模型及其推广版本，原本是一类二维晶格模型。实际量子材料，即便是二维 van der Waals (vdW) 体系或者其它层状化合物体系，面外 out-of-plane 相互作用总是存在的，只是强弱不同而已。将二维 Kitaev 模型 (已经包括了晶体场、SOC 和电子关联等物理成分) 推广到三维 QSL 问题的研究，可能算是最受关注也最直接的推广。对此，以 Kitaev 模型为基础，物理人已经通过考虑各种 bilayer 和 multilayer 结构中面外耦合和相互作用形式进行推演和拓展，获得很多结果。有些尝试甚至得到了严格解，有些则展示了数值计算的新物理。

　　十多年前，在米国斯坦福大学和加州大学伯克利分校学习工作的姚宏 (姚宏现任清华大学教授，他也是南京大学物理系本科校友，与李建新同出龚昌德先生门下)，与量子凝聚态物理名家、伯克利物理系的李东海老师 (Dung-Hai Lee) 一起，提出了他们那个三维 QSL 模型 (应该算是满足 SU(2) 对称性的、基于 Kitaev 模型的推广)，得到了一类严格可解的结果，令人印象深刻。这一模型，展示了包括马约拉纳费米子在内的量子态。特别是，该结果在 QSL 基态基础上展现了 spin-1 的低能激发，有超越 Kitaev 模型的新物理，呈现出更为丰富的效应。Ising 孤陋寡闻且又外行，私底下认为这一模型可能算是这些面向三维推广工作中较有特色和价值的模型之一，现在被同行称为“Yao - Lee model (姚-李模型)”。回顾量子凝聚态物理的诸多工作，华人学者的贡献得到了很好彰显，而这个模型可能是难得的几个以华人凝聚态物理学者命名的模型之一。Ising 自作主张，将 Kitaev 模型和 Yao – Lee 模型的些许内涵整理于图 2 中，读者可前往文库御览详细内容。

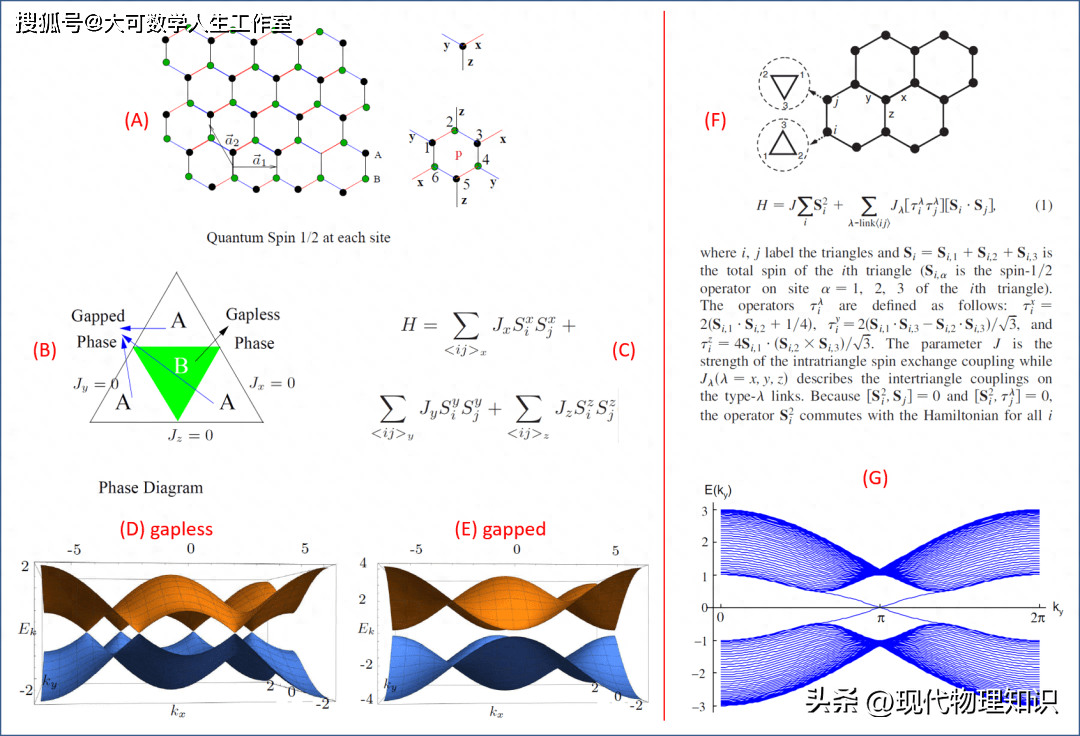
　　右侧：(F) Yao - Lee model 的定义和模型参数说明。(G) Yao - Lee 模型给出的能谱，展示了清晰的边缘无能隙态和新物理。

　　火狐电竞

　　毫无疑问，“姚-李模型”比 Kitaev 更接近实际，包含了更多相互作用和对称性考量。当然，模型所给出的物理预言和背后的深刻讨论较为专业，远非作为外行的 Ising 所能洞察一二。不过，将这一模型推向某个实际的材料体系，并给出明确的物理性质预言，应该是很棒的想法。姚老师他们可能更多站在高处“一览众山小”，具体到一丘一壑是什么样子，那是后来接棒之量子材料人的任务。

　　来自米国亚利桑那州立大学 (Arizona State University) 物理系年轻的理论学者 Onur Erten 教授领衔其课题组 (第一作者 Emilian Nica 博士)，与来自德国马普复杂系统研究所的 Roderich Moessner 教授合作，最近几年开展了 Kitaev 物理的研究，似乎很关注低维 vdW bilayer 魔角物理和 Moire 超晶格中关联量子物理研究。他们将“姚-李模型”应用到以 CrI3 这类 vdW 双层体系为载体的魔角和 Moire 超晶格中，提取出新的模型表示，获得了“姚-李模型”框架下的 QSL 相图，包括一些不错的严格解处理结果，令人印象深刻。

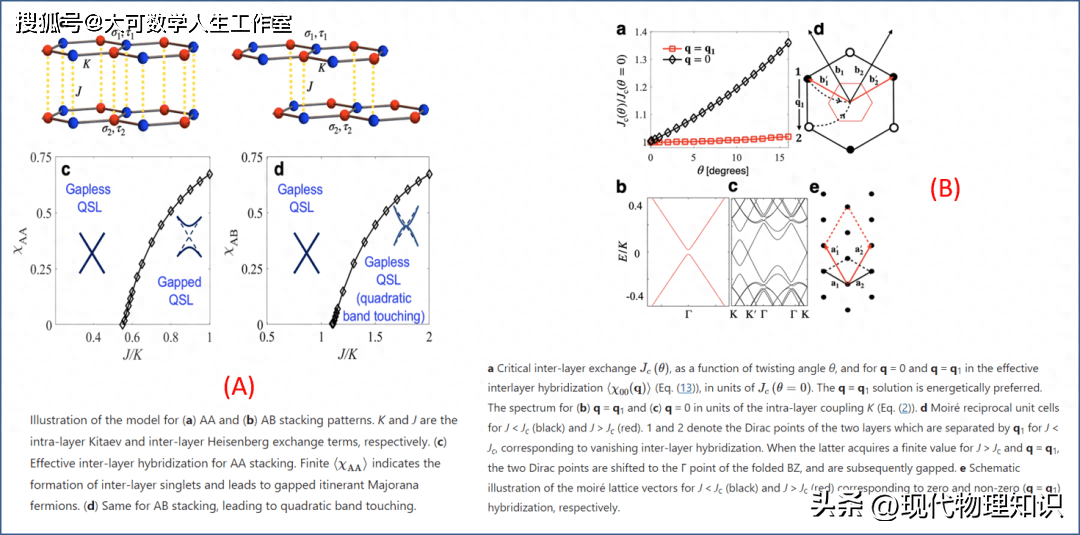
　　图 3. Onur Erten 他们给出的“姚-李模型”在 vdW bilayer 体系中的相图 (A)，此时魔角为零。对 Moire 超晶格的能谱，他们得到的结果显示于 (B) 中。

　　Ising 作为外行，虽多番研读，依然不得要领，只好看热闹一般 highlight 几点读书笔记 (部分结果显示于图 3 所示)：

　　(2) vdW 双层或多层，通过面内转角而形成魔角 Moire 条纹超晶格，能够显著压制载流子动能项，相对意义上显著增强电子相互作用，从而在能谱中引入平带效应。vdW 魔角体系中电子关联的显著贡献，也被坐实了。

　　(3) 从“姚-李模型”的严格解可大致判断，这一模型较好地处理了层间相互作用和自旋 - 轨道耦合物理，并展示具有 Z2 规范对称性的、有能隙磁通激发态 (Z2gauge symmetry with gapped flux excitations) 和边缘无能隙态 (图 2(G) 所示)。更进一步，在“姚-李模型”中，面外耦合与面内磁通激发算符是对易的，因此它们有共同的本征态。这一重要性质使得可以利用“姚-李模型”讨论体系纯粹的低能激发，包括层间耦合引入的自旋单态 (spin - singlet)，从而显著提升“姚-李模型”框架下拓扑 QSL 态的稳定性 (也就是说，在这类魔角体系中，QSL 更容易实现)。

　　(4) 当然，双层魔角堆叠，还与两层堆叠模式有关，包括 AA 堆叠和 AB 堆叠。这些堆叠模式给出的马约拉纳激发能谱有所不同。例如在 AA 堆叠时，很容易实现具有 Z2 对称性的、有能隙的 QSL (gapped Z2 QSL)；而在 AB 堆叠时，马约拉纳费米子是无能隙、可巡游的 (itinerant Majorana fermions)。两种模式都展示了独特的、自旋单态物理，是实现拓扑超导等新物理的良好载体。

　　Onur Erten 和 Emilian Nica 他们的这一工作，继承了“姚-李模型”简洁的风格，更是得益于该模型严格解给出的明确指引，从而能全面和深入地展示双层魔角 vdW体系中可能存在的拓扑 QSL 物理。这样的结果不容易获得，但又因为严格可解而更容易获得，彰显了严格可解模型对量子材料问题的重要贡献。特别是在哈密顿较为复杂、包含了诸多很低能标的低能激发情况下，数值计算往往因为收敛问题和全谱覆盖的困难，可能就难以得到令人完全信服的结果。诸如“姚-李模型”这样可以严格求解的理论，所有低能标物理大概率难以逃脱。Ising 以为，严格可解模型在这里又一次展示了其价值，即便是关联量子体系，即便是非常规超导这样都是低能标物理的领域。